Напомню концепцию:
Есть две части:
- Парабола y = -x² - 2x + 3, но только при x ≥ -2.
- Прямая (о ней позже), действующая при x < -2.
Точка x = -2 — наш разделитель, «переключатель» между двумя формулами.
Сегодня детально разбираем первую часть — параболу.
Шаг 1:
Находим вершину.
Формула для x вершины: x₀ = -b / 2a.
У нас a = -1, b = -2.
Считаем: x₀ = -(-2) / (2 * (-1)) = 2 / (-2) = -1.
Теперь находим y вершины, подставив x₀ = -1 в нашу формулу:
y₀ = -(-1)² - 2*(-1) + 3 = -1 + 2 + 3 = 4.
✅ Вершина параболы имеет координаты (-1; 4). И нам повезло: она попадает в нашу область (x ≥ -2), значит, принадлежит графику.
Итак, вершина найдена.
Ваш ход!
Чтобы построить этот кусок параболы, что будем делать дальше?
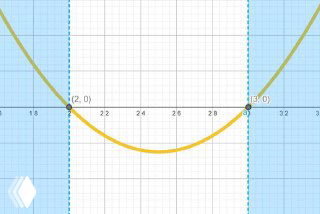
🔎 Подсказка на картинке