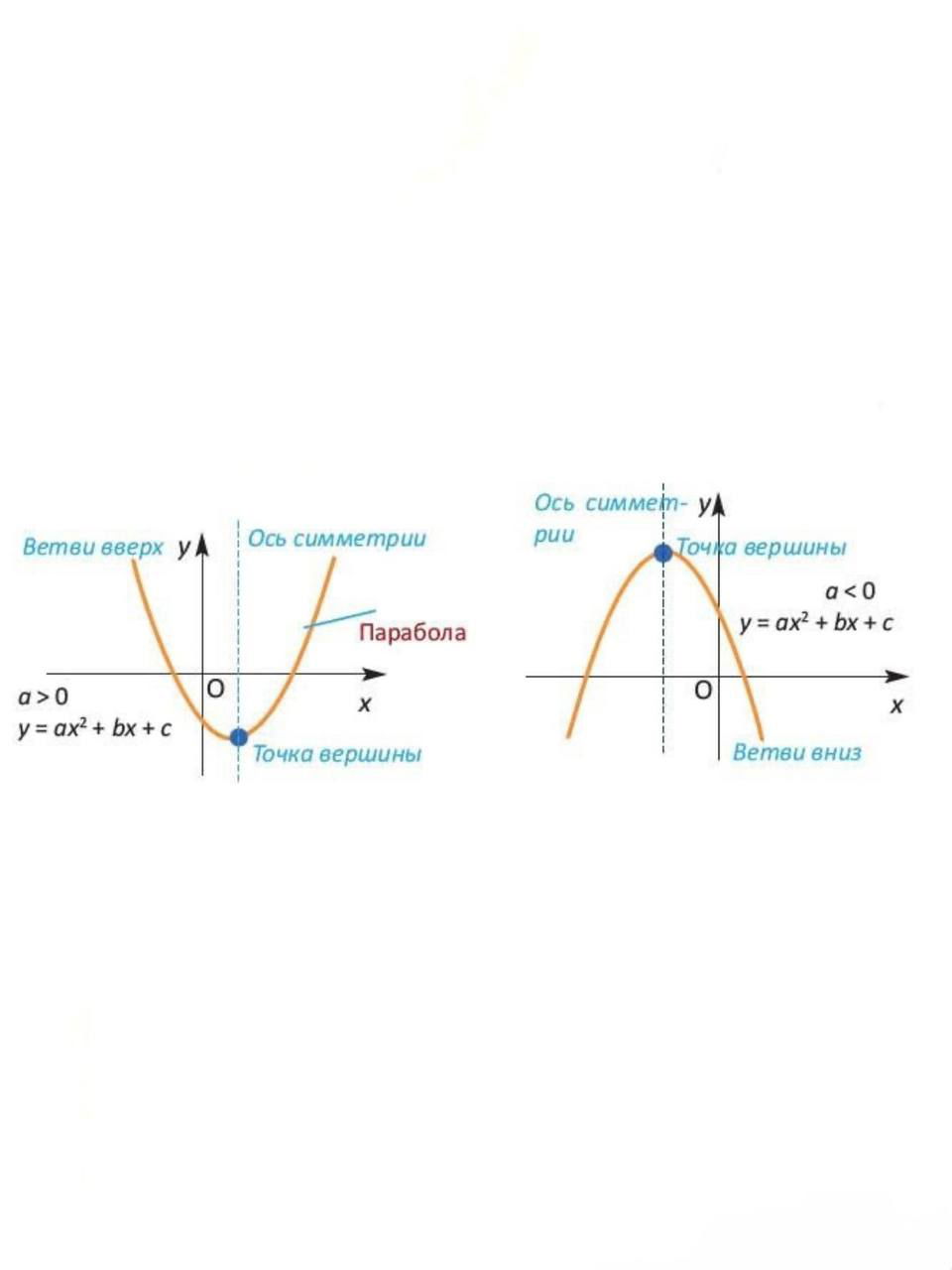
Шаг 2: Направление ветвей параболы...
... y = ax² + bx + c определяется коэффициентом a. В нашем случае перед x² стоит -1 (можно явно записать как y = -1*x² - 2x + 3). Поскольку a = -1 < 0, ветви параболы направлены вниз.
Шаг 3: Ищем пересечение с осью X (нули функции).
Это не всегда обязательно, но рекомендую этот шаг. Он страхует от ошибок в вычислениях и помогает точнее представить форму графика.
Итак, решаем: -x² - 2x + 3 = 0.
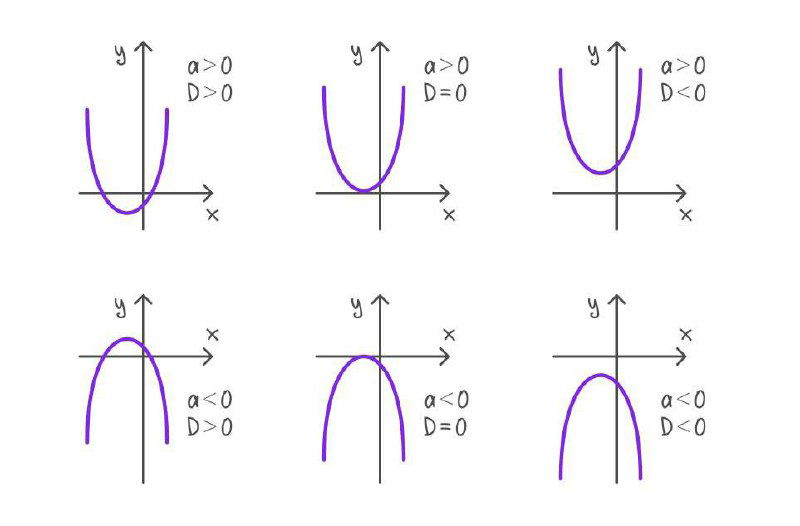
Дискриминант:
D = b² - 4ac = (-2)² - 4 * (-1) * 3 = 4 + 12 = 16.
Поскольку 16 > 0, уравнение имеет два корня (две точки пересечения с осью OX):
x₁ = (-b + √D) / (2a) = (2 + 4) / (2 * (-1)) = 6 / (-2) = -3. Соответствующая точка: (-3; 0).
x₂ = (-b - √D) / (2a) = (2 - 4) / (-2) = (-2) / (-2) = 1. Соответствующая точка: (1; 0).
Накладываем ограничение по области (x ≥ -2):
- 🔹Точка (-3; 0) имеет x = -3. Это меньше -2, значит, она не принадлежит той части параболы, которую мы сейчас строим. Поэтому точку рисовать не будем.
- 🔹Точка (1; 0) имеет x = 1. Это больше -2, значит, она принадлежит нашему графику и будет отмечена.
Таким образом, у нас уже есть:
- Вершина: (-1; 4).
- Направление ветвей: вниз.
- Одна точка на оси OX из нашей области: (1; 0).
Что нужно сделать, чтобы закончить построение параболы? Внимание на картинку!

Дискуссия