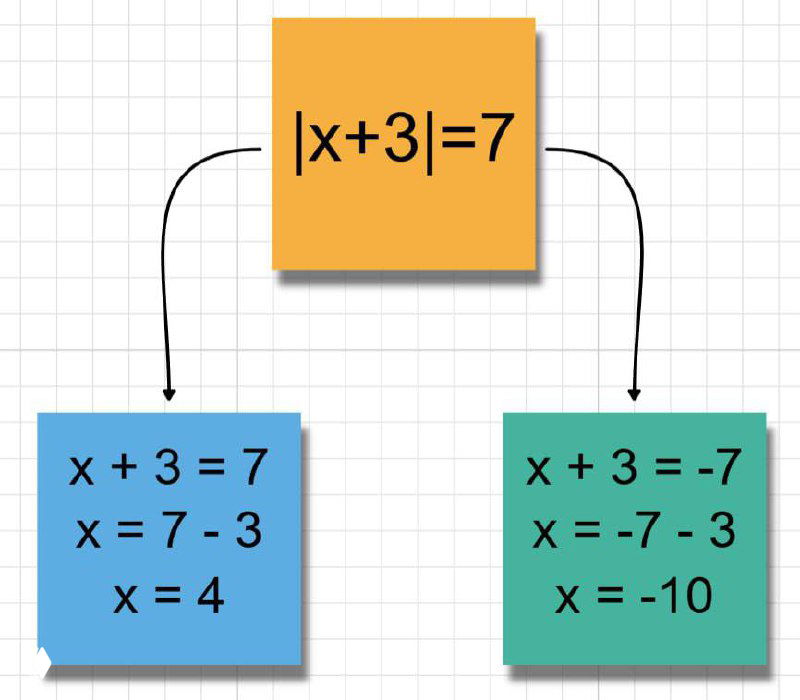Пошагово, как в кулинарной книге.
Правило: Модуль — как двуликий Янус. Если внутри него спрятан x, уравнение всегда имеет два ответы (или ни одного).
Пример 1: |x| = 3
Разбираем:
- Что значит это уравнение?
- •Какие числа находятся на расстоянии 3 от нуля на числовой прямой
- •Видим две точки: 3 (справа от нуля) и -3 (слева от нуля).
- 3. Ответ: x = 3; x = -3.
Почему именно так?
Потому что модуль игнорирует направление. Если бы уравнение было про температуру, это означало бы: "Изменение температуры на 3 градуса — но неважно, потеплело или похолодало".
Пример 2: |x + 2| = 5
Объясняем, как для друга, который никогда не слышал про алгебру:
- Что такое (x + 2)?
- •Это "лифт проехал (x + 2) этажей".
- •Но модуль говорит: "Общее расстояние — 5 этажей".
- Как это перевести на человеческий язык?
- •Лифт мог ехать вверх на 5 этажей → тогда (x + 2) = 5.
- •Или вниз на 5 этажей → тогда (x + 2) = -5 (потому что движение вниз — это отрицательное направление).
- Решаем оба случая:
Случай 1 (вверх):
x + 2 = 5 → x = 5 - 2 → x = 3.
→ Проверяем: |3 + 2| = |5| = 5 ✔️
Случай 2 (вниз):
x + 2 = -5 → x = -5 - 2 → x = -7.
→ Проверяем: |-7 + 2| = |-5| = 5 ✔️
Итог: x = 3; x = -7.
⁉️Почему нельзя написать (x + 2) = ±5?
Потому что это не одно уравнение, а два разных сценария. Их нужно решать по отдельности, как два независимых рецепта.
😨Главные ошибки: почему все путаются?
- "Модуль равен отрицательному числу"
Пример: |x| = -3.
Почему это ошибка?
Модуль — это расстояние.
→ Можно ли пройти -3 метра? Нет!
→ Ответ: нет решений. - "Забыл про минус"
Пример: |x| = 4 → x = 4 и x = -4.
Почему?
Если вы напишете только x = 4 → это как сказать: "Лифт ехал только вверх", хотя он мог и вниз.
→ Всегда проверяйте оба направления! - "Запутался в скобках"
Пример: |x + 3| = 7.
Ошибка: x + 3 = ±7 → x = 4 или x = -10.
Правильно:
x + 3 = 7 → x = 4
x + 3 = -7 → x = -10
→ Нельзя писать ± в уравнении — это два разных уравнения.
💥Потренируйтесь! Разбор полётов
Задача: |x - 1| = 4
Пошаговое решение для самых маленьких:
- Что означает (x - 1)?
Это "лифт проехал (x - 1) этажей".
Модуль говорит: "Общее расстояние — 4 этажа". - Два сценария:
Случай 1 (вверх):
x - 1 = 4 → x = 4 + 1 → x = 5.
→ Проверка: |5 - 1| = |4| = 4 ✔️
Случай 2 (вниз):
x - 1 = -4 → x = -4 + 1 → x = -3.
→ Проверка: |-3 - 1| = |-4| = 4 ✔️
Ответ: x = 5; x = -3.
💡Совет от профессионала:
Всегда подставляйте ответы обратно в уравнение. Это как примерять одежду — вдруг что-то не подойдет?
🎯 Итоги: 5 ключевых правил
- Модуль — это расстояние. Он не может быть отрицательным.
- Если в модуле x → два ответа (кроме случая |x| = 0 → x = 0).
- Раскрывайте модуль на два случая:
- •Внутри модуля положительное число.
- •Внутри модуля отрицательное число.
- Проверяйте оба ответа — иногда один из них может не подходить.
- Рисуйте числовую прямую — это помогает визуализировать.
👉Следующий пост будет: уравнения вида ||x| - 2| = 3 (модуль внутри модуля). Не пропусти!
P.S. Если до сих пор непонятно — представьте, что модуль это ваш друг-оптимист: он всегда говорит: «Неважно, + или −, главное — сколько!» 😊
#репетитор #репетиторпоматематике #модуль #экзамен