Вчера 85% смогли решить задачу с восьмиугольником. Весь секрет был в связи вписанного и центрального угла. Сегодня разложу по шагам, как этот один приём закрывает целых три задачи из ОГЭ.
Это не абстрактная теория. «Переход» от вписанного угла к центральному (и наоборот) — ключевой манёвр, когда данных в задаче катастрофически мало.
Вот как это работает в реальных заданиях.
Запоминайте схему:
🔎 Шаг 1: Видите вписанный угол — ищите его центральную пару
Это основа. Дан угол ∠ABC, вершины которого лежат на окружности? Сразу смотрите на центр O и ищите центральный угол ∠AOC, опирающийся на ту же дугу AC.
Правило на века: Вписанный угол (∠ABC) равен половине центрального (∠AOC) для одной дуги.
🔄 Шаг 2: Делайте «переход» — удваивайте или делите пополам
Это сердце алгоритма.
Если дан вписанный (например, x° в задаче №9) → соответствующий центральный = 2x°.
Если дан центральный (как 45° во вчерашней задаче) → искомый вписанный = 22.5°.
🧩 Шаг 3: Преобразуйте фигуру, используя новые данные
После «перехода» картина меняется! Часто нужно мысленно перестроить фигуру, чтобы увидеть известные углы.
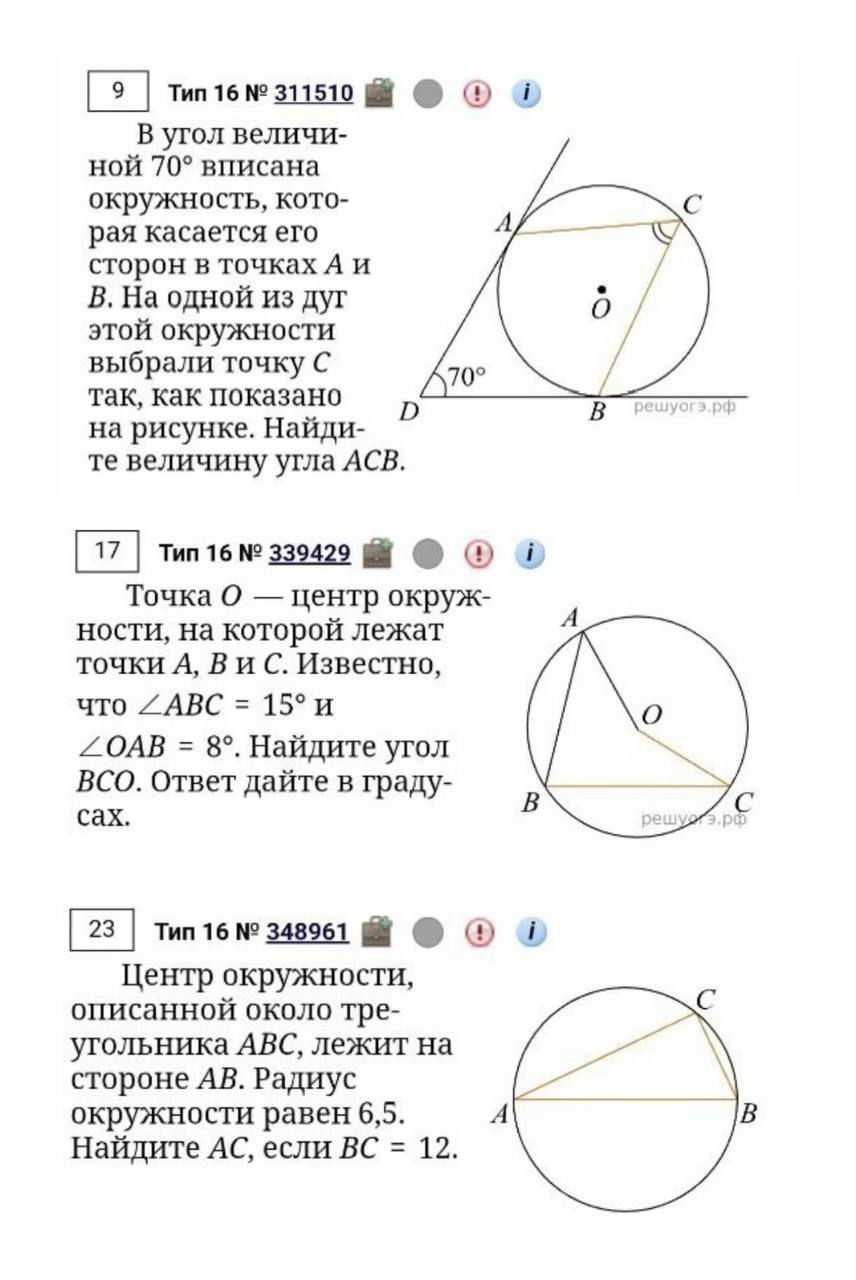
Как в задаче №9: Зная только ∠ACB=x°, переходим к ∠AOB=2x°. Теперь рассматриваем четырёхугольник AOBD. В нём уже два угла по 90° (т.к. OA и OB — радиусы, проведённые к касательным), и третий (∠AOB) мы только что нашли. Задача из нерешаемой стала простой.
Как в задаче №17: Даны два угла. Через переход от вписанного ∠ABC (15°) к центральному ∠AOC (30°) находим часть дуги. Используем, что полная окружность — 360°, и свойство суммы углов в четырёхугольнике — находим недостающий.
✅ Шаг 4: Частный случай — ищите диаметр!
Особая, но частая ситуация: если центр окружности лежит на стороне треугольника, то эта сторона — диаметр. А вписанный угол, опирающийся на диаметр, — прямой (90°).
На примере задачи №23: Если в треугольнике ABC центр O лежит на AB → AB — диаметр →∠AOB — центральный и равен 180° →∠ACB, опирающийся на дугу AB (180°), будет равен 90°. Треугольник мгновенно становится прямоугольным, и решение упрощается.
💬 ВОПРОС К ВАМ:
Какой из этих шагов-манёвров самый сложный для понимания?
Напишите в комментариях:
- 1️⃣ — Шаг 1. Определить, какой угол дан и на какую дугу опирается
- 2️⃣ — Шаг 2. Сам переход «вписанный → центральный»
- 3️⃣ — Шаг 3. Перестроить фигуру и увидеть новую конфигурацию (как с четырёхугольником AOBD)
- 4️⃣ — Шаг 4. Увидеть в условии «центр на стороне» и вспомнить про диаметр

Дискуссия