Вчера мы разобрали базовую задачу на окружность: вы успешно справились.
Сегодня предлагаю перейти к случаю, который часто ставит в тупик даже хорошо подготовленных учеников.
Условие, которое требует внимательного чтения:
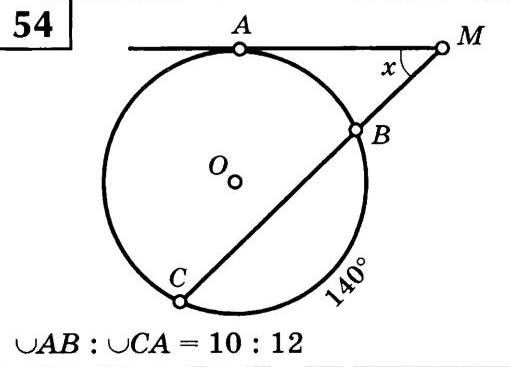
На окружности отмечены три точки: A, B и C.
Известно, что дуга AB относится к дуге AC как 10:12.
Также известно, что дуга BC составляет 140°.
Нужно найти угол между прямыми, проведёнными из точки A.
🤔 ПОЧЕМУ ЭТА ЗАДАЧА ВЫЗЫВАЕТ СТУПОР?
Сложность в том, что непонятно, с чего начать. Множество действий, и кажется, будто нужно строить дополнительные линии, проводить хорды, соединять точки...
Но главная трудность — неочевидность первого шага.
Я в таких случаях предлагаю начать с простого: обозначить неизвестное.
📝 ПОДРОБНЫЙ РАЗБОР:
Шаг 1: Вводим удобные обозначения
Пусть коэффициент пропорции для дуг будет y.
Тогда:
Дуга AB = 10y
Дуга AC = 12yШаг 2: Используем главное свойство окружности
Вся окружность — это 360°.
Дуга AB + дуга AC + дуга BC = 360°
Подставляем:
10y + 12y + 140° = 360°Шаг 3: Решаем простое уравнение
22y + 140° = 360°
22y = 220°
y = 10Шаг 4: Находим конкретные величины дуг
Дуга AB = 10 × 10 = 100°
Дуга AC = 12 × 10 = 120°Шаг 5: Применяем специальную теорему (ту самую, которую часто забывают)❗️
Существует теорема об угле между хордами (или секущими):
Величина угла между двумя прямыми, проведёнными из одной точки окружности, равна полуразности величин дуг, заключённых между хордами этих прямых.
Применяем:
x = (Дуга AC - Дуга AB) / 2
x = (120° - 100°) / 2
x = 10°
Какой момент в задачах на окружность у вас вызывает наибольшие трудности?
💯 - если все понятно
❤️ - непонятно, но очень интересно

Дискуссия