Итак, выяснили, что подобие треугольников — это важная тема. Но как именно доказать, что два треугольника подобны? 🤔
В школьном курсе есть три надежных способа:
- По двум углам
Если два угла одного треугольника соответственно равны двум углам другого — треугольники подобны.
- По двум сторонам и углу между ними
Когда две стороны одного треугольника пропорциональны двум сторонам другого, а углы между этими сторонами равны — это признак подобия.
- По трем сторонам
Если все три стороны одного треугольника пропорциональны трем сторонам другого — такие треугольники подобны.
А теперь — как это работает на практике?📝
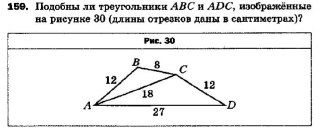
Сравниваем ACD и ABC, выводим пропорции:
- Меньшие : CD = 12 и BC = 8 → 12 ÷ 8 = 1,5
- Средние : AС = 18 и AB = 12 → 18 ÷ 12 = 1,5
- Большие : AD = 27 и AC = 18 → 27 ÷ 18 = 1,5
🎉 Коэффициент везде 1,5! Значит, треугольники ACD и ABC подобны по третьему признаку ✔️
Теперь вы можете легко определять подобие треугольников! 😎

Дискуссия