Вот конкретный пример задачи, которая решается только через их свойства⬇️
📎 Как рассуждаем и решаем:
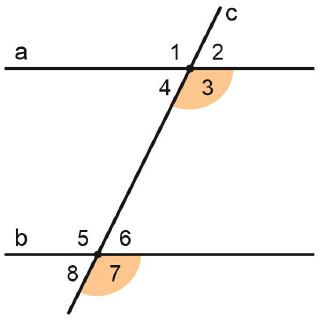
- 1. Находим равные углы.
Посмотрим на угол в 22°. Он расположен на прямой m и на зелёной секущей. У него есть «брат»-угол — на прямой n и на той же секущей. Они называются соответственные. Когда прямые параллельны, как наши m и n, такие углы равны.
➡️ Значит, пустой угол при прямой n тоже равен 22°.
Проще представить: прямые m и n — это как две параллельные железнодорожные рельсы. Зелёная секущая — это путь, который их пересекает. Соответственные углы — это как одинаковые столбы, стоящие на обоих рельсах в одном и том же месте.
- 2. Используем свойство треугольника.
Этот пустой угол (22°) оказывается одним из углов треугольника. В любом треугольнике сумма всех трёх углов всегда 180°.
У нас уже есть два угла этого треугольника:
🔴22° (только что нашли)
🔴72° (дан по условию)Третий угол (наш искомый угол 3) равен: 180° − (22° + 72°) = 86°.
✔️Готово. Задача решается в два логичных шага, и эти баллы можно смело брать.
Здесь работает важное правило: если две прямые параллельны, то соответственные углы равны. Но верно и обратное: если соответственные углы равны, то прямые параллельны.
Эта двусторонняя связь и есть ключ к решению многих задач.
Где чаще всего ошибаются❓
Основная путаница возникает, когда ребята не могут правильно определить, какие именно углы являются соответственными на чертеже и подписывают другие, похожие на них.
Резюмируя:
- Увидели в задаче параллельные прямые: сразу ищите секущую и отметьте все углы.
- Твёрдо выучите три типа углов: соответственные, накрест лежащие, односторонние.
📢 Помните, что у каждого из них, вне зависимости от задачи, одна из сторон будет секущая, а вторая - параллельная прямая.