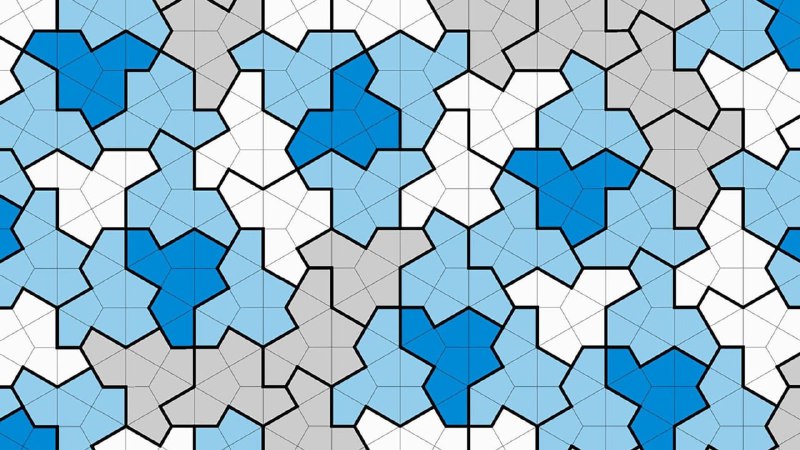
Задача апериодического паттерна была сформулирована в 1960-х. Апериодический — это тот, в котором рисунок нигде не повторяется. Первое решение предлагало набор из 20 тысяч плиток. Позже число фигур в решении сократилось до 92, затем до 6 и 2 плиток. Ещё эти две плитки известны как плитки Пенроуза
Математик-любитель Дэвид Смит обнаружил многоугольник, при помощи которого удалось решить эту задачу. Фигуру, состояюущю из 13 сторон, он назвал «шляпой» из-за сходства с головным убором. По словам учёных, «шляпа» — не новая геометрическая фигура и точно не изобретение Смита, но именно ему первому пришла идея применить её для решения задачи. Чтобы подтвердить своё открытие, Дэвид также проконсультировался с профессиональными коллегами
Статьи об этом решении: популярная и для специалистов
Ещё мы писали про математику: