Вчера мы разобрали параллелограмм, а сегодня — время трапеции.
ШАГ 1
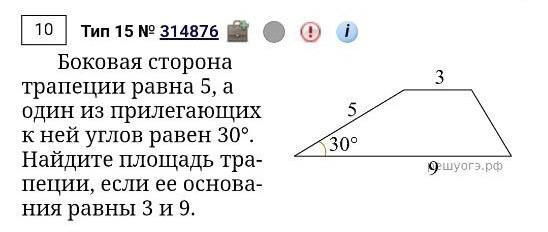
Сначала кажется, что всё просто: площадь трапеции — это полусумма оснований, умноженная на высоту.
Складываем 3 и 9, делим на два — получаем 6. Это полусумма, она же средняя линия. Полдела сделано!
Но потом взгляд упирается в высоту… А её на чертеже нет. Её нужно найти. И здесь многие начинают нервно перебирать формулы.
ШАГ 2
Проводим высоту из левого верхнего угла вниз. Получается прямоугольный треугольник. В нём гипотенуза — это наша боковая сторона (5), а один из углов — тот самый, данный по условию, 30°.
ШАГ 3
И теперь — момент истины. Можно, конечно, вспоминать тригонометрию, синусы… Но есть путь проще.
В прямоугольном треугольнике катет, лежащий напротив угла в 30°, равен половине гипотенузы. Это не формула, это теорема — крепкая и надёжная.
Значит, наша высота — этот самый катет — будет равна половине от 5. Получаем 2,5.
ШАГ 4
А дальше, чистая математика: 6 (полусумма оснований) × 2,5 (высота) = 15.
Всё. Задача решена. Главное было: увидеть тот самый треугольник и вспомнить простое правило про угол в 30°.
❤️ — уже знал(-а) и решал(-а)
🔥 — а, теперь все понятно
😮 — непонятно, но очень интересно
Что разберём завтра: ромб или треугольник?
Пишите в комментариях👇
Дискуссия